Análisis Matemático no Lineal Relacionado a un Modelo de Insulina-Células Pancreáticas en Presencia de Epinefrina
DOI:
https://doi.org/10.17488/RMIB.45.1.2Palabras clave:
diabetes, modelo, células β, LCCIResumen
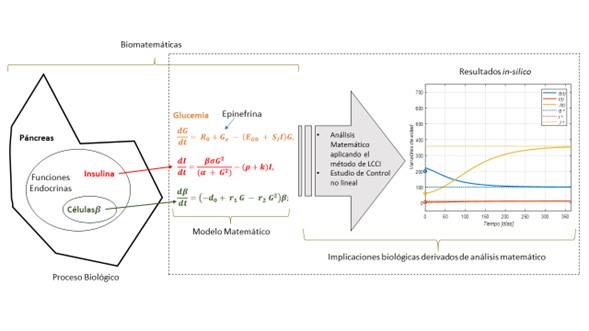
En este trabajo se estudia un modelo de ecuaciones diferenciales ordinarias no lineales que describe la relación entre la masa de células β y la secreción de epinefrina. Se analiza el impacto del estrés asociado como causante de incremento de los niveles de glucosa en el organismo. El análisis matemático se fundamenta en la aplicación de la teoría de control no lineal para definir la capacidad de carga máxima para cada variable de estado, estableciendo un dominio invariante positivo acotado a través del método de Localización de Conjuntos Compactos Invariantes (LCCI). El objetivo es determinar los efectos asociados a la secreción de epinefrina en el aumento de los niveles de glucosa en sangre; por lo tanto, los resultados de este análisis ayudan a definir las condiciones necesarias y suficientes en las que la epinefrina eleva los niveles de insulina y glucosa en presencia de células β. El interés por estudiar este tipo de enfermedades se enfoca en la búsqueda de un tratamiento o un análisis que garantice un control completo de los niveles de glucosa. El desarrollo y análisis matemático de este trabajo fortalece la investigación vigente de diabetes mellitus insulinodependiente entorno a factores críticos de epinefrina que implican un incremento de glucosa en el organismo.
Descargas
Citas
A. Basto-Abreu, N. López-Olmedo, R. Rojas-Martínez, C. A. Aguilar-Salinas, et al., “Prevalencia de prediabetes y diabetes en México: Ensanut 2022,” Salud Publica Mex, vol. 65, pp. s163-s168, jun. 2023, doi: https://doi.org/10.21149/14832
I. I. Mohammed, I. Adamu, S. J. Barka, “Mathematical model for the dynamics of glucose, insulin and β-cell mass under the effect of trauma, excitement and stress,” Model. Numer. Simul. Mater. Sci., vol. 9, no. 4, pp. 71–96, oct. 2019, doi: https://doi.org/10.4236/mnsms.2019.94005
O. A. Montesinos-López, C. M. Hernández-Suarez, “Modelos matemáticos para enfermedades infecciosas,” Salud Publica Mex., vol. 49, no. 3, pp. 218–226, jul. 2007. [En línea]. Disponible en: https://www.scielo.org.mx/scielo.php?script=sci_arttext&pid=S0036-36342007000300007
E. F. Panqueba Moreno, J. M. Ruiz Vera, “Control óptimo de la glucosa en la sangre mediante infusión continua de insulina,” Ciencia Desarro., vol. 13, no. 2, pp. 49-67, jul. 2022, doi: https://doi.org/10.19053/01217488.v13.n2.2022.14173
F. X. Méndez-Carrillo, M. Beléndez-Vázquez, “Variables emocionales implicadas en el control de la diabetes: estrategias de intervención,” An. Psicol., vol. 10, no. 2, pp. 189–198, 1994. [En línea]. Disponible: https://revistas.um.es/analesps/article/view/29671
M. Zahedi, S. Kordrostami, M. Kalantarhormozi, M. Bagheri, “A Review of Hyperglycemia in COVID-19,” Cureus, vol. 15, no. 4, pp. 1-7, 2023, doi: https://doi.org/10.7759/cureus.37487
M. Sirlanci, M. E. Levine, C. C. Low Wang, D. J. Albers, A. M. Stuart, “A simple modeling framework for prediction in the human glucose–insulin system,” Chaos, vol. 33, no. 7, art. no. 073150, jul. 2023, doi: https://doi.org/10.1063/5.0146808
S. V. K. R. Rajeswari, P. Vijayakumar, “Mathematical Approaches in the Study of Diabetes Mellitus,” in Computer Vision and Robotics. Algorithms for Intelligent Systems, Lucknow, India, 2023, pp. 229-248, doi: https://doi.org/10.1007/978-981-19-7892-0_18
J. M. Munoz-Pacheco, C. Posadas-Castillo, E. Zambrano-Serrano, “The effect of a non-local fractional operator in an asymmetrical glucose-insulin regulatory system: Analysis, synchronization and electronic implementation,” Symmetry, vol. 12, no. 9, art. no. 1395, 2023, doi: https://doi.org/10.3390/sym12091395
B. Topp, K. Promislow, G. DeVries, R. M. Miura, D. T. Finegood, “A model of β-cell mass, insulin, and glucose kinetics: pathways to diabetes,” J. Theor. Biol., vol. 206, no. 4, pp. 605–619, oct. 2000, doi: https://doi.org/10.1006/jtbi.2000.2150
D. Laurent, K. F. Petersen, R. R. Russell, G. W. Cline, G. I. Shulman, “Effect of epinephrine on muscle glycogenolysis and insulin-stimulated muscle glycogen synthesis in human,” Am. J. Physiol., vol. 274, no. 1, pp. 130–138, 1998, doi: https://doi.org/10.1152/ajpendo.1998.274.1.E130
D. C. Deibert, R. A. Defronzo, “Epinephrine-induced insulin resistance in man,” J. Clin. Invest., vol. 65, no. 3, pp. 717–721, 1980, doi: https://doi.org/10.1172/JCI109718
A. P. Krishchenko, “Localization of Invariant Compact Sets of Dynamical Systems,” Differ. Equ., vol. 41, no. 12, pp. 1669–1676, 2005, doi: https://doi.org/10.1007/s10625-006-0003-6
D. Gamboa, C. E. Vázquez, P. J. Campos, “Nonlinear Analysis for a Type-1 Diabetes Model with Focus on T-Cells and Pancreatic β-Cells Behavior,” Math. Comput. Appl., vol. 25, no. 2, pp. 23, 2020, doi: https://doi.org/10.3390/mca25020023
D. Gamboa, C. E. Vázquez-López, R. Gutierrez, P. J. Campos, “Nonlinear Analysis of the C-Peptide Variable Related to Type 1-Diabetes Mellitus,” Symmetry, vol. 13, no. 7, pp. 1238, 2021, doi: https://doi.org/10.3390/sym13071238
D. Gamboa, L. N. Coria, P. A. Valle, “Ultimate Bounds for a Diabetes Mathematical Model Considering Glucose Homeostasis,” Axioms, vol. 11, no. 7, art. no. 320, 2022, doi: https://doi.org/10.3390/axioms11070320
A. P. Krishchenko, K. E. Starkov, “Localization of compact invariant sets of the Lorenz system,” Phys. Lett. A, vol. 353, no. 5, pp. 383-388, 2006, doi: https://doi.org/10.1016/j.physleta.2005.12.104
K. E. Starkov, “On dynamic tumor eradication conditions under combined chemical/anti-angiogenic therapies,” Phys. Lett. A, vol. 382, no. 6, pp. 387-393, 2018, doi: https://doi.org/10.1016/j.physleta.2017.12.025
K. Saranya, T. Iswarya, V. Mohan, K. E. Sathappan, L. Rajendran, “Mathematical modeling of Glucose, Insulin, β-Cell Mass: Homotopy Perturbation Method Approach,” Eur. J. Mol. Clin. Med., vol. 07, no. 02, pp. 3513–3530, 2020. [En línea]. Disponible en: https://ejmcm.com/uploads/paper/ca3ad85a4a3175b4f8ac48ac1f80300c.pdf
P. G. Jacobs, P. Herrero, A. Facchinetti, J. Vehi, et al., “Artificial intelligence and machine learning for improving glycemic control in diabetes: best practices, pitfalls and opportunities,” IEEE Rev. Biomed. Eng., pp. 19-41, 2023, doi: https://doi.org/10.1109/RBME.2023.3331297
C. Cobelli, B. Kovatchev, “Developing the UVA/Padova Type 1 Diabetes Simulator: Modeling, Validation, Refinements, and Utility,” J. Diabetes Sci. Technol., vol. 17, no. 6, pp. 1493-1505, 2023, doi: https://doi.org/10.1177/19322968231195081
Publicado
Cómo citar
Número
Sección
Licencia
Derechos de autor 2024 Revista Mexicana de Ingenieria Biomedica

Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial 4.0.
Una vez que el artículo es aceptado para su publicación en la RMIB, se les solicitará al autor principal o de correspondencia que revisen y firman las cartas de cesión de derechos correspondientes para llevar a cabo la autorización para la publicación del artículo. En dicho documento se autoriza a la RMIB a publicar, en cualquier medio sin limitaciones y sin ningún costo. Los autores pueden reutilizar partes del artículo en otros documentos y reproducir parte o la totalidad para su uso personal siempre que se haga referencia bibliográfica al RMIB. No obstante, todo tipo de publicación fuera de las publicaciones académicas del autor correspondiente o para otro tipo de trabajos derivados y publicados necesitaran de un permiso escrito de la RMIB.











